문제 URL : https://programmers.co.kr/learn/courses/30/lessons/42894
코딩테스트 연습 - 블록 게임
[[0,0,0,0,0,0,0,0,0,0],[0,0,0,0,0,0,0,0,0,0],[0,0,0,0,0,0,0,0,0,0],[0,0,0,0,0,0,0,0,0,0],[0,0,0,0,0,0,4,0,0,0],[0,0,0,0,0,4,4,0,0,0],[0,0,0,0,3,0,4,0,0,0],[0,0,0,2,3,0,0,0,5,5],[1,2,2,2,3,3,0,0,0,5],[1,1,1,0,0,0,0,0,0,5]] 2
programmers.co.kr
문제 접근법 :

N*N 사이즈 배열에서
위와같은 블록들이 놓여져있을때
검은색 블록을 떨어뜨려 직사각형을 만들수있을때
제거할수있는블록들이 최대 몇개를 제거할수있는지 물어보는 문제입니다.
놓여져있는 블록은 움직이지않습니다. 실제로 모양을 보면

이렇게 생긴 모양들만 제거를 할수 있겠지만 일일이 그런거 생각하는게 더 코드가 길어지고 복잡합니다.
한마디로 말해서 귀찮습니다.
그럼 어떻게 제거할수있을까요?
어떤블록이든 직사각형 안에 들어갈수있도록 만들어본다면

채워져있는 블록의 좌표들중 가장 작은 y값 좌표와 x값 좌표는 y,x-1이고
가장 큰y값 좌표가 x값좌표는 y+1,x+1입니다.
즉

이런식의 직사각형안에 채워졌을때 검은색 블록으로 채워졌을때 직사각형내에 모든 블록들이 채워져있는지 확인만 하면되는거겠죠
이런 문제는 위클리 챌린지3주차 풀이에서도 똑같이 했었던 풀이이니
https://congsoony.tistory.com/170
프로그래머스 퍼즐 조각 채우기(위클리 챌린지 3주차)
문제 URL : https://programmers.co.kr/learn/courses/30/lessons/84021 코딩테스트 연습 - 3주차 [[1,1,0,0,1,0],[0,0,1,0,1,0],[0,1,1,0,0,1],[1,1,0,1,1,1],[1,0,0,0,1,0],[0,1,1,1,0,0]] [[1,0,0,1,1,0],[1,0,..
congsoony.tistory.com
여기서도 잘 확인해보시길 바랍니다.
그런식으로 다른색들의 블록들을 담아서
검은색 블록을 한꺼번에 떨어뜨립니다. 이런식으로

왼쪽그림과 같은 블록이 놓여져있을때 검은색블록을 한꺼번에 떯어뜨리면 오른쪽 블록과같이 되는 그림을 보여드렸습니다.
그렇다면 왼쪽과 파랑색블록과 오른쪽 빨간색블록이 직사각형으로 채워져있으니 지워주면되겠죠?
그리고 마지막으로 검은색 블록들까지 다지워주면 다른블록들을 또제거할수있는지 알수있겟죠?
그치만 검은색블록을 한번떨어뜨리면 아래와같은그림은 제거할수가없게됩니다.
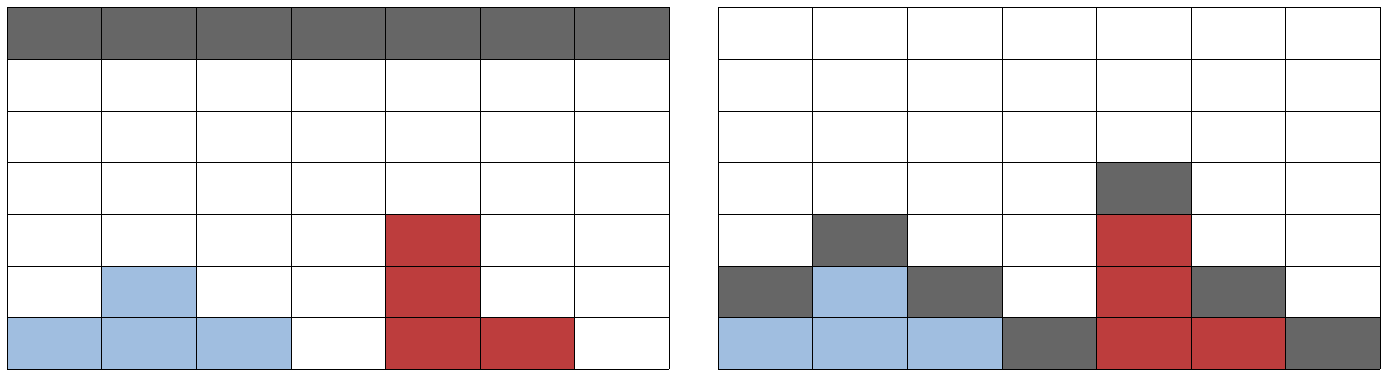
오른쪽 은 아직 다채워지지 직사각형으로 채울수있지만 전부 채워지지않았기에
검은색블록을 2번을 떯어뜨려야 오른쪽을 제거할수있습니다.

이렇게 2번을 떯어뜨려야 채워진 사각형을 제대로 만들수있습니다. 이것을 몇번해야할까요?
처음에 1번만떯어뜨리다가 왜틀린지 몰라서 계속 확인해보니 2번을 떯어뜨려야한다는것을 망각했었습니다.
그렇다면 이것을 몇번해야할까요??
이문제에 원소가 200이하라고 했으니 이런식으로 200개를 제거할수있으니 200번을 해야겠죠?
소스코드 :
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
|
//By 콩순이냉장고
#include <bits/stdc++.h>
using namespace std;
#define v vector
#define vi v<int>
#define vvi v<vi>
#define vvvi v<vvi>
#define pii pair<int,int>
#define vpii v<pii>
#define M 200
int dy[4] = { -1,0,1,0 };
int dx[4] = { 0,1,0,-1 };
vvi check, Board;
int n;
pii minb[M+1], maxb[M+1];
vpii blocks[M+1];
vi colors(M + 1);
bool isrange(int y, int x) {
return 0 <= y && y < n && 0 <= x && x < n;
}
void dfs(int y, int x, int color) {
if (!isrange(y, x))return;
if (Board[y][x] == 0)return;
if (check[y][x] || Board[y][x] != color)return;
check[y][x] = 1;
for (int i = 0; i < 4; i++)
dfs(y + dy[i], x + dx[i], color);
blocks[color].push_back({ y,x });
}
void fall(vvi& temp) {
for (int i = 0; i < n; i++) {
if (temp[0][i] == 0) {
temp[0][i] = -1;
int y = 0, x = i;
int ny = y+dy[2];
int nx = x + dx[2];
while (isrange(ny, nx) && temp[ny][nx] == 0) {
swap(temp[ny][nx], temp[y][x]);
tie(y, x, ny, nx) = make_tuple(ny, nx, ny + dy[2], nx + dx[2]);
}
}
}
}
bool iserase(int color,vvi& temp) {
int cnt = 0;
int h = maxb[color].first - minb[color].first + 1;
int w = maxb[color].second - minb[color].second + 1;
for (int i = minb[color].first; i <= maxb[color].first; i++) {
for (int j = minb[color].second; j <= maxb[color].second; j++) {
if (temp[i][j] == color || temp[i][j] == -1)
cnt++;
}
}
return cnt == h * w;
}
void Erase() {
for (int i = 0; i < M; i++) {
vvi temp = Board;
fall(temp);
fall(temp);
for (int j = 1;j <= M; j++) {
if (colors[j] == 0)continue;
if (iserase(j, temp)) {
for (int k = 0; k < blocks[j].size(); k++)
Board[blocks[j][k].first][blocks[j][k].second] = 0;
colors[j] = 0;
}
}
}
}
int solution(vector<vector<int>> board) {
int answer = 0;
n = board.size();
Board = board;
check = vvi(n, vi(n));
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
dfs(i, j, Board[i][j]);
colors[Board[i][j]] = 1;
}
}
colors[0] = 0;
for (int i = 1; i <= M; i++) {
if (colors[i] == 0)continue;
answer += colors[i];
minb[i] = blocks[i][0];
maxb[i] = blocks[i][0];
for (int j = 0; j < 4; j++) {
minb[i].first = min(minb[i].first, blocks[i][j].first);
minb[i].second = min(minb[i].second, blocks[i][j].second);
maxb[i].first = max(maxb[i].first, blocks[i][j].first);
maxb[i].second = max(maxb[i].second, blocks[i][j].second);
}
}
Erase();
for (int i = 1; i <= M; i++) {
answer -= colors[i];
}
return answer;
}
|
cs |

궁금한점 혹은 모르는점 논리적인 오류등 어떤질문이든 댓글은 언제나 환영입니다.
공감도 눌러주실꺼죠?
'프로그래머스' 카테고리의 다른 글
| 프로그래머스 무지의 먹방 라이브(2019 KAKAO BLIND RECRUITMENT) (0) | 2021.09.05 |
|---|---|
| 프로그래머스 [1차] 셔틀버스(2018 KAKAO BLIND RECRUITMENT) (0) | 2021.09.05 |
| 프로그래머스 매칭 점수(2019 KAKAO BLIND RECRUITMENT) (0) | 2021.09.01 |
| 프로그래머스 블록 이동하기(2020 KAKAO BLIND RECRUITMENT) (0) | 2021.08.31 |
| 프로그래머스 가사 검색(2020 KAKAO BLIND RECRUITMENT) (0) | 2021.08.23 |



